Runge Romberg's method. Solution of differential equations. See the meaning of the Romberg Method in other dictionaries

Numerical integration problem consists in replacing the original integrand f(x), for which it is difficult or impossible to write the antiderivative in analytics, by some approximating function φ(x). Such a function is usually a polynomial (piecewise polynomial). I.e:
,
where - a priori error of the method on the integration interval,
but r(x) is the a priori error of the method at a separate integration step.

Overview of integration methods.

Methods for calculating one-time integrals are called quadrature(for multiple integrals - cubature).

Rectangle method.

Distinguish between the method of left, right and middle rectangles. The essence of the method is clear from the figure. At each integration step, the function is approximated by a polynomial of degree zero - a segment parallel to the x-axis.

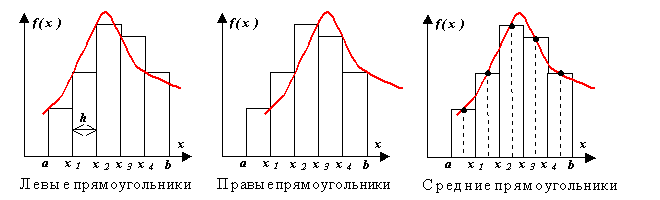
Let us derive the formula of the method of rectangles from the analysis of the decomposition of the function f(x) into a Taylor series near some point x = x i.

Consider the range of integration from x i before x i +h, where h is the integration step.

Calculate …=

== . Got the formula right (or left) rectangles and a priori error estimate r at a separate integration step. The main criterion by which the accuracy of the algorithm is judged is the degree of the step size in the formula for the a priori error estimate.

In case of an equal step h over the entire range of integration general formula has the form

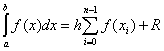Here n is the number of partitions of the integration interval, 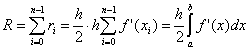. For the validity of the existence of this estimate, the existence of a continuous f "(x) is necessary.

Method of middle rectangles . Here, on each interval, the value of the function is considered at the point , i.e. . The expansion of the function in a Taylor series shows that in the case of medium rectangles, the accuracy of the method is much higher:

Trapezoidal method.

Approximation in this method is carried out by a polynomial of the first degree. The essence of the method is clear from the figure.

On a single interval
.
In the case of a uniform grid ( h= const)

Wherein , but 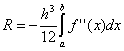. The error of the trapezoidal method is twice as high as that of the mean rectangle method! However, in practice, it is possible to find the average value on an elementary interval only for functions specified analytically (and not tabularly), therefore, it is far from always possible to use the method of average rectangles. Due to different signs of error in the formulas of trapezoids and middle rectangles, the true value of the integral usually lies between these two estimates.

Features of the behavior of the error.

It would seem that why analyze different methods of integration if we can achieve high accuracy by simply reducing the value of the integration step. However, consider the graph of the behavior of the a posteriori error R results of numerical calculation depending on and from the number n interval partitions (that is, at step . In section (1), the error decreases due to a decrease in step h. But in section (2), the computational error begins to dominate, accumulating as a result of numerous arithmetic operations. Thus, for each method there is its own Rmin, which depends on many factors, but primarily on the a priori value of the error of the method R.

Refinement formula of Romberg.

The Romberg method consists in successive refinement of the value of the integral with a multiple increase in the number of partitions. The formula of trapezoids with a uniform step can be taken as the base h.
Denote the integral with the number of partitions n= 1 as .
Decreasing the step by half, we get .
If we successively reduce the step by 2 n times, we get a recursive relation for calculating .

Let us calculate four times the integral with n from 1 to 4. Imagine the following triangle:
R(1;1)
R(2;1) R(2;2)
R(3;1) R(3;2) R(3;3)
R(4;1) R(4;2) R(4;3) R(4;4)

The first column contains the values of the integral obtained by successively doubling the number of intervals. The following columns are the results of refining the value of the integral using the following recursive formula:

The lower right value in the triangle is the desired refined value of the integral.

Simpson method.

Integrand f(x) is replaced by an interpolation polynomial of the second degree P(x) - a parabola passing through three nodes, for example, as shown in the figure ((1) - function, (2) - polynomial).

Consider two steps of integration ( h= const = x i+1 – x i), that is, three nodes x0, x1, x2, through which we draw a parabola, using Newton's equation:
.
Let be z = x - x0,
then

Now, using the obtained relation, we calculate the integral over this interval:

.

Let it be required to calculate the definite integral on the interval .

Not always the problem can be solved analytically. In particular, a numerical solution is required when the integrand is given in a table. For numerical integration, the integrand is approximated by some simpler function, the integral of which can be calculated. Usually, a polynomial is used as an approximating function. In the case of a polynomial of degree zero, the method of numerical integration is called rectangle method , in the case of a polynomial of the first degree - trapezoidal method , in the case of a polynomial of the second degree - Simpson's method . All these methods are special cases. Newton-Cotes quadrature formulas .

So, in the trapezoid method, the integrand is approximated by a polynomial of the first degree, that is, a straight line. This means that instead of the area of a curvilinear trapezoid, we will look for the area of a rectangular trapezoid. The approximate value of the integral is

The error of this formula is .

Let's denote where . The meaning of the introduced designation will become clear somewhat later.

The estimate of the value of the integral can be made more accurate by dividing the interval into n parts and apply the trapezoid formula for each such interval

If we divide the interval into two parts, that is, if we reduce the step by half, then the estimate for the value of the integral will look like

In this case, the summation includes only one element. Please note that the old estimate is included in the new estimate. We needed to define the value of the function only at new nodes.

If there are 2 n subintervals, then

If n=0 then

If n=1 then

If n=2 then

In general, the recurrence relation is valid

The resulting relation is called the recursive trapezoid formula and is often used to calculate certain integrals. The advantage of this formula is that as the number of subintervals increases, the function only needs to be calculated at the newly added points. Unfortunately, with the help of this formula it is impossible to obtain an arbitrarily exact value of the integral. First, as the number of partitions increases, the amount of computation increases rapidly; secondly, at each step, a rounding error is accumulated. To further refine the value of the integral, the following step can be taken − extrapolate the resulting sequence of values in the case of an infinite number of points, or what is the same, in the case of a zero step. This approach is called Romberg's method .

The Romberg method consists in extrapolating the obtained estimates of the value of the integral to the case of an infinite number of partitions (step size equal to zero) according to the recursive formula

That is, the following triangle is built

R(2,1) R(2,2)

R(3,1) R(3,2) R(3,3)

R(4,1) R(4,2) R(4,3) R(4,4)

R(5,1) R(5,2) R(5,3) R(5,4) R(5,5) ,

in which the first column consists of the values of the integral obtained by successively doubling the number of intervals. The second column is the result of refining the values of the first column using a recursive formula. The third column is the refined values of the integral based on the second column, and so on.

Differential equations are very often encountered in the construction

models of the dynamics of objects of study. They describe, as a rule, changes in the parameters of an object over time. result solutions differential equations are functions, and not numbers, as in solving finite equations, as a result of which the methods for solving them are more laborious.

Differential equations also describe the process, heat and mass transfer, changes in the concentration of a substance, sugar crystallization processes, and many others. When using numerical methods for solving differential equations:

Or y ’ = f (x, y) is presented in tabular form, i.e. it turns out
dx set of values Y i and X i .

The solution is step-by-step, i.e. one or more initial points (x, y) in one step find the next point, etc. The difference between two adjacent values of the argument h = x i +1 - x i is called step.

The Cauchy problems are most widely used, in which the initial conditions are given: for x = x 0 , y(x 0) = y 0 . Having them, it is easy to start the solution process, i.e. find at x 1, y 2 - at x 2, etc.

The main idea of obtaining the simplest computational algorithms in one-step methods is reduced to the expansion of the original solution y(x) in a Taylor series.

The number of terms left in the series determines the order and therefore the accuracy of the method. According to the decomposition obtained, knowing the values of y at the decomposition point y i and the derivative f(x i , y i ), the values of y are found through the step h:
y i +1 = y i + ∆y i .

If more terms are retained in the expansion, then it is necessary to calculate f(x i , y i) at several points (in this way, the need to directly calculate the higher derivatives present in the expansion in a Taylor series is avoided).

The calculation algorithms of multi-step methods are based on the construction of interpolation or approximating functions, from which the integral is taken.

Numerical methods solve not only individual equations, but also systems of equations (most often of the first order), and most of the methods for solving one equation are easily extended to solving systems.

The class of one-step methods includes the Euler methods,
Runge-Kutta and Euler-Koshi.

Functional Equation y¢ = f(x, y), which links the independent variable, the desired function y(x) and its derivative y(x), is called differential equation of the 1st order.

A (partial) solution of an equation on the interval (a, b) is any function at= (X), which, being substituted into this equation together with its derivative ¢ (x) turns it into an identity with respect to xО (a,b). The equation F. (x, y) = 0, which defines this solution as an implicit function, is called the integral of the differential equation. On a plane with a fixed Cartesian rectangular system coordinate equation Ф (х, y) =0 defines some curve, which is called the integral curve of the differential equation.

If in the differential equation y¢ = f(x, y) function f(x, y) continuous in some area D, plane Ohu and has a bounded partial derivative in this region (x,y), then for any point (x 0 ,y 0) О D, in some interval x 0 - h £ x £ x 0+ h, there is a unique solution y(x) of this equation, satisfying the initial condition

y (x o) - y o.

This statement is known as the Cauchy theorem on the existence and uniqueness of a solution to a differential equation with a given initial condition.

For tasks of this type, separated into a whole class Cauchy problems, in addition to analytical solution methods, numerical solution methods have been developed.

Euler method

Values of the desired function y=y(x) on the segment is found by the formula:

y k+1 = y k + h×f(x k , y k), (1)

where y k \u003d y (x k), x k + 1 \u003d x k + h, (x n \u003d X), k \u003d 0,1,2, ... n -1 and h \u003d

For a given limiting absolute error e, the initial calculation step h is set using the inequality h 2< .

Euler-Cauchy method

To calculate function values y=y(x) apply the formula:

(2)

where , , ,

For a given marginal error, the initial calculation step h is set using the inequality h 3 < .

Ruge-Kutta method

Values of the desired function y=y(x) on the segment are sequentially found by the formulas:

y k +] = y k + y k , k = 0, l, 2,...n – l (3)

where y k = (),

r a v i l o R o m berg a, method calculation of a definite integral, based on Richardson extrapolation. Let the value I of a certain functional be calculated, and the calculated approximate value of T(h) depends on the parameter h, so that the result of the calculation is an approximate equality. Let information about the behavior of the difference I - T(h) be known. as a function of h, namely: (1) where m - natural number and a depends on the functional being approximated and the function on which it is calculated, on the method of approximation, and (weakly) on h. If T(2h) is calculated along with T(h), then the Richardson method gives for I the approximation (2) This approximation is the better, the weaker a from equality (1) depends on h. In particular, if a does not depend on h, then (2) also satisfies the exact equality. R. m. is applied to the calculation of the integral. The interval is taken for simplicity of notation, it can be any finite. Let (3) Calculations in R. m. reduce to compiling the following table: where the first column consists of quadrature sums (3) of the trapezoid formula. The elements of the (l+2)th column are obtained from the elements of the (l+l)th column according to the formula (4) When compiling the table, the main part of the computational work is spent on calculating the elements of the first column. The elements of the following columns are calculated a little more complicated than finite differences. Each element of the table is a quadrature sum approximating the integral (5) The nodes of the quadrature sum are points, and its coefficients are positive numbers. Quadrature formula (5) is exact for all polynomials of degree at most 2l+1.
Assuming that the integrand f(x) has a continuous derivative of order 2l+2 on , the difference has a representation of the form (1), in which m=2l+2. It follows that the elements of the (l+2)th column calculated by formula (4) are Richardson improvements of the elements of the (l+l)th column. In particular, the representation holds for the error of the quadrature trapezoid formula, and Richardson's method gives a more accurate approximation to I: it turns out to be the quadrature sum of Simpson's formula, and since the representation holds for the error of this formula, we can again use the Richardson method, etc. In P m., T 0n is taken as an approximation to I, and it is assumed that there exists a continuous derivative f(2n) (x) on . An approximate idea of the accuracy of the approximation of T 0p can be obtained by comparing T0n and T1, n_1. The method was first described by V. Romberg. Lit.: [l] R ombe rg W., "Kgl. norske vid. selskabs forhandl.", 1955, Bd 28, no. 7, s. 30-36; In a u e r F. L., R u t i s h a u s e r H., Stiefl E, "Proq. Symp. Appl. Math.", 1963, v. 15, p. 199-218. I. P. Mysovskikh.

Watch value Romberg Method in other dictionaries

Method- m. and method. method, order, grounds; the accepted way to move, to achieve something, in the form of general rules. -dicic, decent, correct, thorough, gradual;........
Dahl's Explanatory Dictionary

Method- (new official). Abbreviation, use in new compound words ah in meaning. methodical, for example. method bureau.
Explanatory Dictionary of Ushakov

Method M. And Ustar. Method J.— 1. Method of cognition, approach to the study of natural phenomena and social life. 2. Reception, a system of receptions in some. areas of activity.
Explanatory Dictionary of Efremova

Method...- 1. The initial part of compound words, introducing the meaning of the word: methodical (method bureau, method cabinet, method association, etc.).
Explanatory Dictionary of Efremova

Analytical Forecasting Method— A forecasting method based on obtaining expert estimates by logical analysis of the predictive model.
Political vocabulary

Behavioral Method- (from the English "behavior" - behavior) - in political science involves the study of political phenomena and processes through the analysis of the behavior of individuals and groups in the performance ........
Political vocabulary

Delphi Method, Delphi Method— Method of collective peer review, based on the identification of an agreed assessment of the expert group by their autonomous survey in several rounds, providing for ........
Political vocabulary

Matrix Prediction Method— A forecasting method based on the use of matrices that reflect the values (weights) of the vertices of the graph model of the forecasting object, followed by transformation of the matrices........
Political vocabulary

Method- - means of analysis, a method of testing and evaluating knowledge.
Political vocabulary

Destructive Referred Appraisal Method– The method of collective generation of ideas, implemented through two sessions spaced during sessions, the first of which is completely subject to the rules of collective generation ........
Political vocabulary

Method of Individual Expert Evaluation— A forecasting method based on using one expert as a source of information.
Political vocabulary

Method Interview— The method of individual expert evaluation, based on a conversation between an expert and a forecaster according to the "question-answer" scheme.
Political vocabulary

Method of Historical Analogy— A forecasting method based on the establishment and use of the analogy of the object of forecasting with an object of the same nature, which is ahead of the first in its development.
Political vocabulary

Collective Idea Generation Method— The method of collective peer review, based on stimulating the creative activity of experts through a joint discussion of a specific problem, regulated by ........
Political vocabulary

Collective Peer Review Method- A forecasting method based on the identification of a generalized objectified assessment of the expert group by processing individual, independent assessments made by ........
Political vocabulary

Method of Mathematical Analogy— A forecasting method based on establishing the analogy of mathematical descriptions of the development processes of objects of different nature with subsequent use ........
Political vocabulary

Method for Building a Predictive Scenario— An analytical forecasting method based on establishing a logical sequence of states of the forecasting object and the forecasting background in time at ........
Political vocabulary

Prediction Method- A method of studying the object of forecasting, aimed at developing forecasts. Note. Forecasting methods are the basis for forecasting techniques.
Political vocabulary

Psycho-Intellectual Idea Generation Method- The method of individual expert assessment, in which the identification of expert assessment is carried out with the help of programmed control, including an appeal to ........
Political vocabulary

Guided Idea Generation Method— The method of collective generation of ideas using purposeful intellectual influence (enhancing or suppressing) on the process of generating ideas.
Political vocabulary

Heuristic Prediction Method— An analytical method of forecasting, which consists in constructing and then truncating an expert evaluation search tree using some kind of heuristic.
Political vocabulary

Expert Panel Method- The method of collective expert assessment, which consists in the joint work of experts united in a commission, developing a document on the prospects for the development of the forecasting object.
Political vocabulary

Forward Forecasting Method— A forecasting method based on the use of the property of scientific and technical information to get ahead of the implementation of scientific and technological achievements in social practice.
Political vocabulary

Patent Prediction Method— An advanced forecasting method based on the assessment (according to the accepted system of criteria) of inventions and the study of the dynamics of their patenting.
Political vocabulary

Publication Prediction Method— An advanced forecasting method based on the evaluation of publications about the object of forecasting (according to the accepted system of criteria) and the study of the dynamics of their publication.
Political vocabulary

Synoptic Method— A forecasting method based on the analysis by experts of a known set of forecasts of the forecast object and the forecast background, followed by their synthesis.
Political vocabulary

System Method In Political Science- - consideration of politics as a holistic, complexly organized, self-adjusting mechanism in constant interaction with the environment.
Political vocabulary

Comparative Method In Political Science- - comparison of the same type of political phenomena and processes and identification of their common features and specifics in order to find the optimal forms of political organization or by solving problems.
Political vocabulary

Statistical Prediction Method— Factographic forecasting method based on the construction and analysis of time series of the characteristics of the forecasting object.
Political vocabulary

Factual Forecasting Method— A forecasting method based on the use of sources of factual information.
Political vocabulary