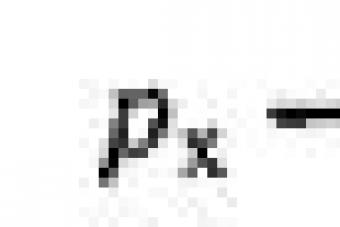Classification of signals and their parameters.
Electrical signals are electrical processes used to transmit or store information.
Signals can be divided into two large classes: deterministic and random. Deterministic signals are those whose instantaneous values at any moment of time can be predicted with a probability equal to one and which are given in the form of a certain definite function of time. Here are some typical examples: a harmonic signal with a known amplitude A and period T(fig. 1.1 but); subsequence rectangular pulses with a known period T, duration t and and amplitude A(fig. 1.1 b); sequence of pulses of arbitrary shape with known duration t and amplitude A and period T(fig. 1.1 in). Deterministic signals do not contain any information.
Random signals are chaotic functions of time, the values of which are unknown in advance and cannot be predicted with a probability equal to unity (a single pulse with duration t and and amplitude A(fig. 1.1 G) speech, music in the expression of electrical quantities). Noise also belongs to random signals.
Deterministic signals, in turn, are subdivided into periodic ones, for which the condition S(t)=S(t + kT), where T- period, k-any integer, and under S(t) means the current, voltage or charge changing over time (Fig.1.1 a B C).
Obviously, any deterministic signal for which the condition S(t)¹ S(t + kT).
The simplest periodic signal is a harmonic signal of the form 
.
Any complex periodic signal can be decomposed into harmonic components. Below, such a decomposition will be carried out for several specific types of signals.
A high-frequency harmonic signal, in which information is embedded by modulation, is called a radio signal (Fig.1.1 d).
Periodic signals.
Any complex periodic signal S(t)=S(t + kT) (Figure 1.2), set on the range of values t from - ¥ to + ¥, can be represented as a sum of elementary harmonic signals. This representation is carried out in the form of a Fourier series, if only the given periodic function satisfies the Dirichlet conditions:
1. At any finite time interval, the function S(t) must be continuous or have a finite number of discontinuities of the first kind.
2. Within one period, the function must have a finite number of maxima and minima.
Typically, all real RF signals meet these conditions. In trigonometric form, the Fourier series has the form (1.1)
where the constant component is 
(1.2)
and the coefficients a n, and b n for cosine and sinusoidal terms of the expansion are determined by the expressions 
(1.3)
Amplitude (modulus) and phase (argument) nth harmonics are expressed in terms of the coefficients a n, and b n in the following way 
(1.4)
When using the complex form of writing, the expression for the signal S (t) takes the form 
... Here the coefficients 
, called complex amplitudes, are equal to 
and are related to the values a n and b n by the formulas: for n> 0, and for n<0. С учётом обозначений 
.
The spectrum of a periodic function consists of separate lines corresponding to discrete frequencies 0, w, 2w, 3w ..., that is, it has a linear or discrete character (Fig. 1.3). The use of Fourier series in combination with the principle of superposition is a powerful tool for analyzing the effect of linear systems on the passage of various types of periodic signals through them.
When expanding a periodic function in a Fourier series, one should take into account the symmetry of the function itself, since this makes it possible to simplify the calculations. Depending on the type of symmetry, the functions represented by the Fourier series can:
1. 
Do not have a constant component if the area of the figure for the positive half-period is equal to the area of the figure for the negative half-period.
2. Not to have even harmonics and constant component, if the values of the function are repeated after half the period with the opposite sign.
Spectral composition of a sequence of rectangular pulses at different periods of their duty cycle.
A periodic sequence of rectangular pulses is shown in Fig. 1.4. The constant component of the Fourier series is determined from the expression and for this case is equal to 
.
Amplitude of cos-components a n is equal to
, and the amplitude of the sin-component b n is equal to 
.
Amplitude n-th harmonic 
Consider a periodic sequence of rectangular pulses with a period T, pulse duration and maximum value 
... Let us find the series expansion of such a signal by choosing the origin as shown in Fig. 15. in this case, the function is symmetric about the ordinate axis, i.e. all coefficients of sinusoidal components 
= 0, and only the coefficients need to be calculated 
.
-
0
T t
constant component 
(28)
The constant component is the average value over the period, i.e. this is the area of the momentum 
divided by the entire period, i.e. 
, i.e. the same as for a rigorous formal calculation (28).
Recall that the frequency of the first harmonic 1 = 
, where T is the period of the rectangular signal. Distance between harmonics = 1. If the harmonic number n turns out to be such that the argument of the sine 
, where 
... The number of the harmonic at which its amplitude turns to zero for the first time is called "First zero" and denote it with the letter N, emphasizing the special properties of this harmonic:
(29)
on the other hand, the duty cycle S of the pulses is the ratio of the period T to the duration of the pulses t u, i.e. 
... Therefore, the "first zero" is numerically equal to the duty cycle of the pulse N=
S... Since the sine vanishes for all values of the argument that are multiples of , then the amplitudes of all harmonics with numbers that are multiples of the “first zero” number also vanish. I.e 
at 
, where k- any integer. So, for example, from (22) and (23) it follows that the spectrum of rectangular pulses with a duty cycle of 2 consists only of odd harmonics. Because the S=2
, then N=2
, i.e. the amplitude of the second harmonic turns to zero for the first time - this is the “first zero”. But then the amplitudes of all other harmonics with numbers that are multiples of 2, i.e. all even ones must also vanish. With a duty cycle S = 3, zero amplitudes will be at 3, 6, 9, 12,…. Harmonics.
With an increase in the duty cycle, the "first zero" shifts to the region of harmonics with large numbers and, therefore, the rate of decrease in the amplitudes of the harmonics decreases. Simple calculation of the amplitude of the first harmonic at U m= 100V for duty cycle S=2, U m 1 = 63.7B, at S=5, U m 1 = 37.4B and at S=10, U m 1 = 19.7B, i.e. with increasing duty cycle, the amplitude of the first harmonic decreases sharply. If we find the ratio of the amplitude, for example, of the 5th harmonic U m 5 to the amplitude of the first harmonic U m 1 then for S=2, U m 5 /U m 1 = 0.2, and for S=10, U m 5 / U m 1 = 0.9, i.e. the decay rate of higher harmonics decreases with increasing duty cycle.
Thus, as the duty cycle increases, the spectrum of the sequence of rectangular pulses becomes more uniform.
2.5. Spectra with decreasing pulse duration and signal period.
Adjust duty cycle S= T/ t n you can either change the pulse duration t n at T= const, or by changing the period T at t n= const. Consider the signal spectra in this case.
T = const,t n = var. First harmonic frequency f 1 =1/ T= const and f= f 1 = const. First zero N= T/ t n and as the pulse shortens t n shifts to the area of harmonics with higher numbers. At t n 0 N, the spectrum is discrete and f= f 1 , infinitely wide and with infinitesimal amplitudes of harmonics.
t n = const,T = var. We will increase the period T, then the frequency of the first harmonic is f 1 and the distance between the spectral lines f will decrease. As f= f 1 = 1 / T, then the spectral lines will shift towards lower frequencies and the "density" of the spectrum will increase. If T, then the signal from periodic to non-periodic (single pulse). In this case f 1 = f0, i.e. the spectrum from discrete turns into a continuous one, consisting of an infinitely large number of spectral lines located at infinitely small distances from each other.
Hence the rule follows: Periodic signals generate discrete (line) spectra, and non-periodic signals generate continuous (continuous) ones.
When passing from a discrete spectrum to a continuous one, the Fourier series is replaced by the Fourier integral. This replacement is most easily performed if we use the notation of the Fourier series in complex form (16) and (17). The Fourier integral for the continuous spectrum is written
, (30)
where 
(31)
Function F(j ) called spectral function or spectral density, which depends on the frequency. Formulas (30) and (31) together are called one-sided Fourier transform, which is a special case of the more general Laplace transform and is obtained by replacing the complex variable in the Laplace transform R on the j .
The spectral function can be represented as the envelope of the coefficients of the Fourier series, i.e. as the limit of the line spectrum of a periodic function at T. Function F(j
)
can be real or complex. Considering in the general case 
, we get two frequency characteristics: 
-amplitude spectrum, i.e. the dependence of the amplitude of the spectral components on the frequency, and
(
)
– phase spectrum, i.e. the law of changing the phase of the spectral components of the signal versus frequency. It can be shown that the amplitude spectrum is always even, and the phase spectrum is always an odd function
.
The spectral function for many non-periodic signals (single pulses of various shapes) is most easily and simply found using tables of originals and images in the Laplace transform, which are given in the educational and reference literature. After finding the Laplace image F(p)
for a given non-periodic function f(t)
, the spectral function is found
(32)
So, according to (30), the non-periodic function f(t)
is represented by a set of an infinitely large number of harmonics with infinitely small amplitudes 
in the entire frequency range from - to +, i.e. performance f(t)
in the form of a Fourier integral implies the summation of undamped harmonic oscillations of an infinite continuous spectrum of frequencies.
laboratory setup description
The work is performed on the "Signal Synthesizer" block, the functional diagram of which is shown in Fig. sixteen.
The block contains generators G1-G6 of the six first harmonics of the signal. The frequency of the first harmonic is 10 kHz. The harmonic signal from the output of the n-th generator through the phase shifter Ф n and the attenuator А n is fed to the adder. Phase shifters set the initial phases of n harmonics, and attenuators - their amplitudes А n.
At the output of the adder, in the general case, the sum of six signal harmonics is obtained
.
From the output of the adder, the signal is fed to the Y input of the oscilloscope. For its external synchronization, a special pulse signal is used, supplied from the "Sync." to the input X of the oscilloscope. To set and control the amplitudes of harmonics, it is possible to turn off any of the harmonics. By turning on only the generator of the n-th harmonic, you can set its amplitude with the attenuator А n and estimate its values using an oscilloscope. Each phase shifter with a switch allows you to set the required discrete value of the initial phase of the harmonic, or turn off the generator.
SIGNALS
Let's consider a few examples of periodic oscillations that are often used in various radio engineering devices.
1. RECTANGULAR VIBRATION (FIG. 2.3)
Such an oscillation, often called a meander, is especially widely used in measurement technology.
When choosing the start of countdown in accordance with Fig. 2.3, and the function is odd, and Fig. 2.3, b - even. Applying formulas (2.24), we find for an odd function (Fig. 2.3, a) with s (t) = e (t):
Rice. 2.3. Periodic rectangular oscillation (meander)
Rice. 2.4. The coefficients of the complex (a) and trigonometric (b) Fourier series of the oscillation shown in Fig. 2.3
Taking into account that, we get
The initial phases in accordance with (2.27) are equal for all harmonics.
Let us write the Fourier series in trigonometric form
The spectrum of the coefficients of the complex Fourier series is shown in Fig. 2.4, a, and the trigonometric series - in Fig. 2.4, b (at).
When counting the time from the middle of the pulse (Fig. 2.3, b), the function is even with respect to t and for it
Graphs of the 1st harmonics and their sums are shown in Fig. 2.5, a. In fig. 2.5, b, this sum is supplemented by the 5th harmonic, and in Fig. 2.5, c - 7th.
With an increase in the number of summed harmonics, the sum of the series approaches the function everywhere, except for the points of discontinuity of the function, where an outlier is formed. When the value of this outlier is equal, i.e., the sum of the series differs from the given function by 18%. This convergence defect in mathematics is called the Gibbs phenomenon.
Rice. 2.5. Summation of the 1st and 3rd harmonics (a), 1st, 3rd and 5th harmonics (b), 1st, 3rd, 5th and 7th harmonics (c) of the oscillation shown in Fig. 2.3
Rice. 2.6 Periodic oscillation of the sawtooth shape
Rice. 2.7. The sum of the first five harmonics of the oscillation shown in Fig. 2.6
Despite the fact that, in the case under consideration, the Fourier series does not converge to the function being expanded at the points of its discontinuity, the series converges on average, since at the outliers are infinitely narrow and do not make any contribution to the integral (2.13).
2. SAW VIBRATION (FIG. 2.6)
Functions like this are often dealt with in oscilloscope scanners. Since this function is odd, the Fourier series for it contains only sinusoidal terms. Using formulas (2.24) - (2.31), it is easy to determine the coefficients of the Fourier series. Omitting these calculations, we write the final expression for the series
As you can see, the amplitudes of the harmonics decrease according to the law, where. In fig. 2.7 shows a graph of the sum of the first five harmonics (enlarged).
3. SEQUENCE OF UNIPOLAR TRIANGULAR PULSES (FIG. 2.8)
The Fourier series for this function is as follows:
Rice. 2.8. Sum of the first three harmonics of a periodic function
Rice. 2.9. Periodic sequence of rectangular pulses with high duty cycle
In fig. 2.8 shows the sum of the first three terms of this series. In this case, we note a more rapid decrease in the amplitudes of the harmonics than in the previous examples. This is due to the absence of breaks (jumps) in the function.
4. SEQUENCE OF UNIPOLAR RECTANGULAR PULSES (FIG. 2.9)
Applying formula (2.32), we find the average value (constant component)
and harmonic distortion
In this section, we will consider the spectrum of a periodic sequence of rectangular pulses, as one of the most important signals used in practical applications.
Spectrum of a periodic sequence of rectangular pulses
Let the input signal be a periodic sequence of rectangular pulses of amplitude, duration of seconds following with a period of seconds, as shown in Figure 1
Figure 1. Periodic sequence of rectangular pulses
The unit of measure for signal amplitude depends on the physical process that describes the signal. It can be voltage, or, current, or any other physical quantity with its own unit of measurement, which changes over time as. In this case, the units of measurement of the amplitudes of the spectrum,, will coincide with the units of measurement of the amplitude of the original signal.
Then the spectrum of this signal can be represented as:
The spectrum of a periodic sequence of rectangular pulses is a set of harmonics with an envelope of the form 
.
Spectrum properties of a periodic sequence of rectangular pulses
Let us consider some properties of the envelope of the spectrum of a periodic sequence of rectangular pulses.
The constant component of the envelope can be obtained as a limit:
To disclose uncertainty, we will use L'Hôpital's rule:
Where is called the duty cycle and sets the ratio of the pulse repetition period to the duration of a single pulse.
Thus, the zero frequency envelope is equal to the pulse amplitude divided by the duty cycle. As the duty cycle increases (i.e., as the pulse width decreases with a fixed repetition period), the envelope value at zero frequency decreases.
Using the duty cycle, expression (1) can be rewritten as:
The zeros of the envelope of the spectrum of a sequence of rectangular pulses can be obtained from the equation:
The denominator vanishes only when, however, as we found out above 
, then the solution to the equation will be
Then the envelope vanishes if
Figure 2 shows the envelope of the spectrum of a periodic sequence of rectangular pulses (dashed line) and the frequency ratios of the envelope and discrete spectrum.
Figure 2. Spectrum of a periodic sequence of rectangular pulses
The amplitude envelope, amplitude spectrum, and phase envelope and phase spectrum are also shown.From Figure 2, you can see that the phase spectrum takes on values when the envelope is negative. Note that and correspond to the same point of the complex plane equal to.
An example of a spectrum of a periodic sequence of rectangular pulses
Let the input signal be a periodic sequence of rectangular amplitude pulses following with a period of a second and different duty cycle. Figure 3a shows time oscillograms of the indicated signals, their amplitude spectra (Figure 3b), as well as continuous envelopes of the spectra (dashed line).
Figure 3. Spectrum of a periodic sequence of rectangular pulses at different values of the duty cycle
a - time oscillograms; b - amplitude spectrum
As you can see from Figure 3, with increasing signal duty cycle, the pulse duration decreases, the spectrum envelope expands and decreases in amplitude (dashed line). As a result, the number of spectrum harmonics increases within the main lobe.
Spectrum of a time-shifted periodic sequence of rectangular pulses
Above, we studied in detail the spectrum of a periodic sequence of rectangular pulses for the case when the original signal was symmetrical with respect to. As a result, the spectrum of such a signal is real and is given by expression (1). Now we will consider what happens to the spectrum of the signal if we shift the signal in time, as shown in Figure 4.
Figure 4. Time-shifted periodic sequence of rectangular pulses
An offset signal can be thought of as a signal delayed by half the pulse width. 
... The spectrum of the shifted signal can be represented according to the cyclic time shift property as:
Thus, the spectrum of a periodic sequence of rectangular pulses shifted from zero is not a purely real function, but acquires an additional phase factor 
... The amplitude and phase spectra are shown in Figure 5.
Figure 5. Amplitude and phase spectra of a time-shifted periodic sequence of rectangular pulses
It follows from Figure 5 that the shift of the periodic signal in time does not change the amplitude spectrum of the signal, but adds a linear component to the phase spectrum of the signal.
conclusions
In this section, we have obtained an analytical expression for the spectrum of a periodic sequence of rectangular pulses.
We examined the properties of the envelope of the spectrum of a periodic sequence of rectangular pulses and gave examples of spectra at different values of the duty cycle.
The spectrum with a time shift of a sequence of rectangular pulses was also considered and it was shown that a time shift changes the phase spectrum and does not affect the amplitude spectrum of the signal.
Moscow, Soviet radio, 1977, 608 p.Dötsch, G. A guide to the practical application of the Laplace transform. Moscow, Nauka, 1965, 288 pp.
From the output of the message source, signals are received that carry information, as well as clock signals used to synchronize the operation of the transmitter and receiver of the transmission system. Information signals are in the form of non-periodic, and clock signals are in the form of a periodic sequence of pulses.
To correctly assess the possibility of transmitting such pulses through communication channels, let us determine their spectral composition. A periodic signal in the form of pulses of any shape can be expanded in a Fourier series according to (7).
For transmission over air and cable communication lines, signals of various shapes are used. The choice of one form or another depends on the nature of the transmitted messages, the frequency spectrum of the signals, the frequency and time parameters of the signals. Signals similar in shape to rectangular pulses are widely used in the technology of transmitting discrete messages.
Let's calculate the spectrum, i.e. the set of amplitudes of constant and
harmonic components of periodic rectangular pulses (Figure 4, a) with duration and period. Since the signal is an even function of time, then in expression (3) all even harmonic components vanish ( 
= 0), and the odd components take on the values:
(10)
The constant component is
(11)
For a 1: 1 signal (CW dots) Figure 4a:
,
.
(12)
Moduli of the amplitudes of the spectral components of a sequence of rectangular pulses with a period 
are shown in Fig. 4, b. The abscissa shows the main pulse repetition rate 
() and frequencies of odd harmonic components 
,
etc. The envelope of the spectrum changes according to the law.
With an increase in the period, in comparison with the pulse duration, the number of harmonic components in the spectral composition of the periodic signal increases. For example, for a signal with a period (Figure 4, c), we obtain that the constant component is equal to and
In the frequency band from zero to frequency, there are five harmonic components (Figure 4, d), while there is only one.
With a further increase in the pulse repetition period, the number of harmonic components becomes more and more. In the limiting case when 
the signal becomes a non-periodic function of time, the number of its harmonic components in the frequency band from zero to frequency increases to infinity; they will be located at infinitely close frequency distances; the spectrum of the non-periodic signal becomes continuous.
Figure 4
2.4 Single pulse spectrum
A single video pulse is set (Figure 5):
Figure 5
The Fourier series method allows for a deep and fruitful generalization, which makes it possible to obtain the spectral characteristics of non-periodic signals. To do this, mentally supplement a single pulse with the same pulses, periodically following at a certain time interval, and we obtain the previously studied periodic sequence:
Let's imagine a single pulse as the sum of periodic pulses with a large period.
,
(14)
where are integers.
For periodic oscillation
.
(15)
In order to return to a single impulse, let us direct the repetition period to infinity:. In this case, it is obvious:
,
(16)
We denote
.
(17)
The quantity is called the spectral characteristic (function) of a single pulse (direct Fourier transform). It depends only on the temporal description of the impulse and, in general, is complex:
, (18) where 
; (19)
; (20)
,
where 
- modulus of the spectral function (amplitude-frequency characteristic of the pulse);
- phase angle, phase-frequency characteristic of the pulse.
We find for a single pulse by formula (8) using the spectral function:
.
If, we get:
.
(21)
The resulting expression is called the inverse Fourier transform.
The Fourier integral defines momentum as an infinite sum of infinitesimal harmonic components located at all frequencies.
On this basis, one speaks of a continuous (continuous) spectrum possessed by a single pulse.
The total energy of the pulse (the energy released on the active resistance Ohm) is equal to
(22)
Changing the order of integration, we get
.
The inner integral is the spectral function of the momentum taken with the argument -, i.e. is a complex conjugate quantity: 
Consequently
Modulus squared (the product of two conjugate complex numbers is equal to the modulus squared).
In this case, it is conventionally said that the pulse spectrum is two-sided, i.e. is located in the frequency band from to.
The above relation (23), which establishes the relationship between the pulse energy (at a resistance of 1 Ohm) and the modulus of its spectral function, is known as Parseval's equality.
It claims that the energy contained in a pulse is equal to the sum of the energies of all its spectrum components. Parseval's equality characterizes an important property of signals. If some electoral system passes only part of the signal spectrum, attenuating its other components, then this means that part of the signal energy is lost.
Since the square of the modulus is an even function of the variable of integration, then by doubling the value of the integral, integration can be introduced in the range from 0 to:
.
(24)
In this case, they say that the spectrum of the pulse is located in the frequency band from 0 to and is called one-sided.
The integrand in (23) is called the energy spectrum (spectral energy density) of the pulse
It characterizes the distribution of energy over frequency, and its value at a frequency is equal to the pulse energy per 1 Hz frequency band. Consequently, the pulse energy is the result of integrating the energy spectrum of the signal over the entire frequency range separately; in other words, the energy is equal to the area enclosed between the curve representing the energy spectrum of the signal and the abscissa axis.
To estimate the distribution of energy over the spectrum, use the relative integral function of the distribution of energy (energy characteristic)
,
(25)
where 
is the pulse energy in a given frequency band from 0 to, which characterizes the fraction of the pulse energy concentrated in the frequency range from 0 to.
For single impulses of various shapes, the following regularities are fulfilled:
