Whatever real number t is taken, it can be assigned a uniquely defined number sin t. True, the correspondence rule is rather complicated; as we saw above, it consists in the following.
To find the value of sin t by the number t, you need:
1) position the number circle in the coordinate plane so that the center of the circle coincides with the origin of coordinates, and the starting point A of the circle hits the point (1; 0);
2) find a point on the circle corresponding to the number t;
3) find the ordinate of this point.
This ordinate is sin t.
In fact, we are talking about the function u = sin t, where t is any real number.
All these functions are called trigonometric functions of the numerical argument t.
There are a number of relationships connecting the values of various trigonometric functions, we have already received some of these relationships:
sin 2 t + cos 2 t = 1
From the last two formulas, it is easy to obtain a relation connecting tg t and ctg t:
All of these formulas are used in those cases when, knowing the value of any trigonometric function, it is required to calculate the values of the remaining trigonometric functions.
The terms "sine", "cosine", "tangent" and "cotangent" were actually familiar, however, they were still used in a slightly different interpretation: in geometry and physics, they considered sine, cosine, tangent and cotangent g l a(but not
numbers, as it was in the previous paragraphs).
It is known from geometry that the sine (cosine) of an acute angle is the ratio of the leg of a right triangle to its hypotenuse, and the tangent (cotangent) of an angle is the ratio of the legs of a right triangle. A different approach to the concepts of sine, cosine, tangent and cotangent was developed in the previous paragraphs. In fact, these approaches are interrelated.
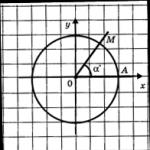
Let's take an angle with a degree measure b o and arrange it in the model "numerical circle in a rectangular coordinate system" as shown in Fig. 14

corner top compatible with center
circles (with the origin of the coordinate system),
and one side of the corner is compatible with
positive ray of the x-axis. Point
intersection of the other side of the angle with
the circle will be denoted by the letter M. Ordina-
Figure 14 b o , and the abscissa of this point is the cosine of the angle b o .
To find the sine or cosine of the angle b o it is not at all necessary to make these very complex constructions each time.
It suffices to note that the arc AM is the same part of the length of the numerical circle as the angle b o is from the angle of 360°. If the length of the arc AM is denoted by the letter t, then we get:
In this way,
For instance,
It is believed that 30 ° is a degree measure of an angle, and is a radian measure of the same angle: 30 ° = rad. Generally:
In particular, I'm glad from where, in turn, we get.
So what is 1 radian? There are various measures of segment lengths: centimeters, meters, yards, etc. There are also various measures to indicate the magnitude of the angles. We consider the central angles of the unit circle. An angle of 1° is a central angle based on an arc that is part of a circle. An angle of 1 radian is a central angle based on an arc of length 1, i.e. on an arc whose length is equal to the radius of the circle. From the formula, we get that 1 rad \u003d 57.3 °.
Considering the function u = sin t (or any other trigonometric function), we can consider the independent variable t as a numerical argument, as was the case in the previous paragraphs, but we can also consider this variable as a measure of the angle, i.e. angular argument. Therefore, speaking of a trigonometric function, in a certain sense it is indifferent to consider it a function of a numerical or angular argument.
Lesson and presentation on the topic: "Trigonometric function of a numerical argument, definition, identities"
Additional materials
Dear users, do not forget to leave your comments, feedback, suggestions. All materials are checked by an antivirus program.
Teaching aids and simulators in the online store "Integral" for grade 10
Algebraic problems with parameters, grades 9–11
Software environment "1C: Mathematical constructor 6.1"
What will we study:
1. Definition of a numeric argument.
2. Basic formulas.
3. Trigonometric identities.
4. Examples and tasks for independent solution.
Definition of the trigonometric function of a numeric argument
Guys, we know what sine, cosine, tangent and cotangent are.Let's see if it is possible to find the values of other trigonometric functions through the values of some trigonometric functions?
Let's define the trigonometric function of a numerical element as: $y= sin(t)$, $y= cos(t)$, $y= tg(t)$, $y= ctg(t)$.
Let's remember the basic formulas:
$sin^2(t)+cos^2(t)=1$. By the way, what is the name of this formula?
$tg(t)=\frac(sin(t))(cos(t))$, for $t≠\frac(π)(2)+πk$.
$ctg(t)=\frac(cos(t))(sin(t))$, for $t≠πk$.
Let's derive new formulas.
Trigonometric identities
We know the basic trigonometric identity: $sin^2(t)+cos^2(t)=1$.Guys, let's divide both sides of the identity by $cos^2(t)$.
We get: $\frac(sin^2(t))(cos^2(t))+\frac(cos^2(t))(cos^2(t))=\frac(1)(cos^2 (t))$.
Let's transform: $(\frac(sin(t))(cos(t)))^2+1=\frac(1)(cos^2(t)).$
We get the identity: $tg^2(t)+1=\frac(1)(cos^2(t))$, with $t≠\frac(π)(2)+πk$.
Now we divide both sides of the identity by $sin^2(t)$.
We get: $\frac(sin^2(t))(sin^2(t))+\frac(cos^2(t))(sin^2(t))=\frac(1)(sin^2 (t))$.
Let's transform: $1+(\frac(cos(t))(sin(t)))^2=\frac(1)(sin^2(t)).$
We get a new identity that is worth remembering:
$ctg^2(t)+1=\frac(1)(sin^2(t))$, for $t≠πk$.
We managed to get two new formulas. Remember them.
These formulas are used if, by some known value of a trigonometric function, it is required to calculate the value of another function.
Solving examples for trigonometric functions of a numerical argument
Example 1$cos(t) =\frac(5)(7)$, find $sin(t)$; $tg(t)$; $ctg(t)$ for all t.
Solution:
$sin^2(t)+cos^2(t)=1$.
Then $sin^2(t)=1-cos^2(t)$.
$sin^2(t)=1-(\frac(5)(7))^2=1-\frac(25)(49)=\frac(49-25)(49)=\frac(24) (49)$.
$sin(t)=±\frac(\sqrt(24))(7)=±\frac(2\sqrt(6))(7)$.
$tg(t)=±\sqrt(\frac(1)(cos^2(t))-1)=±\sqrt(\frac(1)(\frac(25)(49))-1)= ±\sqrt(\frac(49)(25)-1)=±\sqrt(\frac(24)(25))=±\frac(\sqrt(24))(5)$.
$ctg(t)=±\sqrt(\frac(1)(sin^2(t))-1)=±\sqrt(\frac(1)(\frac(24)(49))-1)= ±\sqrt(\frac(49)(24)-1)=±\sqrt(\frac(25)(24))=±\frac(5)(\sqrt(24))$.
Example 2
$tg(t) = \frac(5)(12)$, find $sin(t)$; $cos(t)$; $ctg(t)$, for all $0 Solution: Attention! The slide preview is for informational purposes only and may not represent the full extent of the presentation. If you are interested in this work, please download the full version. Lesson Objectives: Lesson type: training. Type of lesson: skill development lesson. Form of study: group. Group type:
group sitting together. Pupils of different levels of learning, awareness in this subject, compatible students, which allows them to complement and enrich each other. Equipment: board; chalk; table "Trigonometer"; route sheets; cards with letters (A, B, C.) to complete the test; crew name plates; evaluation sheets; tables with the names of the stages of the path; magnets, multimedia complex. Pupils sit in groups: 4 groups of 5-6 people. Each group is a vehicle crew with names corresponding to the names of trigonometric functions, headed by a helmsman. Each crew is given a route sheet and the goal is determined: to pass the given route successfully, without errors. The lesson is accompanied by a presentation. The teacher reports the topic of the lesson, the purpose of the lesson, the course of the lesson, the work plan of the groups, the role of the helmsmen. Introductory speech of the teacher: –
Guys! Write down the number and the topic of the lesson: "Trigonometric functions of a numerical argument." Today in the lesson we will learn: For this you need to know: It has long been known that one head is good, but two is better, which is why you work in groups today. It is also known that the road will be mastered by the walking one. But we live in an age of speeds and time is precious, which means we can say this: “The rider will master the road”, so today we will have a lesson in the form of the Mathematical Rally game. Each group is the crew of the car, led by the helmsman. Purpose of the game: The name of the crews corresponds to the brand of the car on which you are making the run. Crews and their coxswains are introduced: Race motto: "Hurry up slowly!" You have to make a run on the "mathematical terrain" with many obstacles. Route sheets were issued to each crew. Crews who know definitions and trigonometric formulas will be able to overcome obstacles. During the run, each coxswain leads the crew, helping and evaluating the contribution of each crew member to overcome the route in the form of "pluses" and "minuses" in the score sheet. For each correct answer, the group receives a “+”, an incorrect “-”. You have to overcome the following stages of the path: I stage. SDA (rules of the road). And so on the way! 1) In each crew, the helmsmen distribute tickets to each crew member with theoretical questions: 2) Collect the "crumbled" formulas. There is a table on a secret board (see below). The crews must adjust the formulas. Each team writes the answer on the board in the form of a line of corresponding letters (in pairs). Answer: ab, vg, de, hedgehog, zi, yk. Oral work: test. On the secret board it is written: task: simplify the expression. Answers are written next to it. Crews determine the correct answers in 1 min. and pick up the corresponding set of letters. Answer: S.V.A. 3 minutes to the crews for a meeting to solve the task, and then the representatives of the crews write the solution on the board. When the representatives of the crews finish writing down the solution of the first task, all the students (together with the teacher) check the correctness and rationality of the solutions and write them down in a notebook. The helmsmen evaluate the contribution of each crew member with the signs "+" and "-" in the evaluation sheets. Tasks from the textbook: –
Your car has broken down. Your car needs to be fixed. Statements are given for each crew, but they contain errors. Find these mistakes and explain why they were made. The statements use trigonometric functions that correspond to the brands of your cars. You are tired and need to rest. While the crew is resting, the helmsmen sum up the preliminary results: they consider the "pluses" and "minuses" of the crew members and the crew as a whole. For students: 3 or more "+" - score "5"; For crews:"+" and "-" cancel each other out. Only the remaining characters are counted. Guess the charade. From numbers you take my first syllable, The word "trigonometry" (from the Greek words "trigonon" - a triangle and "metreo" - I measure) means "measurement of triangles". The emergence of trigonometry is associated with the development of geography and astronomy - the science of the movement of celestial bodies, the structure and development of the universe. As a result of the astronomical observations made, it became necessary to determine the position of the luminaries, calculate distances and angles. Since some distances, for example, from the Earth to other planets, could not be measured directly, scientists began to develop methods for finding relationships between the sides and corners of a triangle, in which two vertices are located on the earth, and the third is a planet or star. Such relationships can be derived by studying various triangles and their properties. That is why astronomical calculations led to the solution (i.e., finding the elements) of the triangle. This is what trigonometry does. The beginnings of trigonometry were discovered in ancient Babylon. Babylonian scientists were able to predict solar and lunar eclipses. Some information of a trigonometric nature is found in the ancient monuments of other peoples of antiquity. To successfully cross the finish line, it remains to tighten up and make a “jerk”. It is very important in trigonometry to be able to quickly determine the values of sin t, cost, tgt, ctg t, where 0 ≤ t ≤ . Close textbooks. The crews alternately name the values of the functions sin t, cost, tgt, ctg t if: Game results. Helmsmen hand over evaluation sheets. The crew that became the champion of the "Mathematical Rally" is determined and the work of the other groups is characterized. The following are the names of those who received marks "5" and "4". Lesson results. - Guys! What did you learn in class today? (simplify trigonometric expressions; find the values of trigonometric functions). What do you need to know for this? - I think that you understand that the formulas need to be well known in order to apply them correctly. You also realized that trigonometry is a very important part of mathematics, as it is used in other sciences: astronomy, geography, physics, etc. Homework: Definition1: The numerical function given by the formula y=sin x is called the sine. This curve is called sinusoid. Function properties y=sin x 2. Function range: E(y)=[-1; one] 3. Parity function: y=sin x – odd,. 4. Periodicity: sin(x+2πn)=sin x, where n is an integer. This function takes the same values after a certain interval. This property of a function is called periodicity. The interval is the period of the function. For the function y=sin x, the period is 2π. The function y=sin x is periodic, with period T=2πn, n is an integer. The smallest positive period T=2π. Mathematically, this can be written as: sin(x+2πn)=sin x, where n is an integer. Definition2: The numerical function given by the formula y=cosx is called the cosine. Function properties y=cos x 1. Function scope: D(y)=R 2. Function scope: E(y)=[-1;1] 3. Parity function: y=cos x is even. 4. Periodicity: cos(x+2πn)=cos x, where n is an integer. The function y=cos x is periodic, with period Т=2π. Definition 3: The numerical function given by the formula y=tg x is called the tangent. Function properties y=tg x 1. Function domain: D(y) - all real numbers except π/2+πk, k is an integer. Because at these points the tangent is not defined. 3. Parity function: y=tg x is odd. 4. Periodicity: tg(x+πk)=tg x, where k is an integer. The function y=tg x is periodic with period π. Definition 4: The numerical function given by the formula y=ctg x is called the cotangent. Function properties y=ctg x 1. Function domain: D(y) - all real numbers, except for πk, k is an integer. Because at these points the cotangent is not defined. 2. The scope of the function: E(y)=R.
$tg^2(t)+1=\frac(1)(cos^2(t))$.
Then $\frac(1)(cos^2(t))=1+\frac(25)(144)=\frac(169)(144)$.
We get that $cos^2(t)=\frac(144)(169)$.
Then $cos^2(t)=±\frac(12)(13)$, but $0
We get: $sin(t)=tg(t)*cos(t)=\frac(5)(12)*\frac(12)(13)=\frac(5)(13)$.
$ctg(t)=\frac(1)(tg(t))=\frac(12)(5)$.Tasks for independent solution
1. $tg(t) = -\frac(3)(4)$, find $sin(t)$; $cos(t)$; $ctg(t)$, for all $\frac(π)(2)
4. $cos(t) = \frac(12)(13)$, find $sin(t)$; $tg(t)$; $ctg(t)$ for all $t$.
Back forward
During the classes
I. Organizational moment.
II stage. Inspection.
III stage. Cross country racing.
IV stage. Sudden stop is an accident.
V stage. Halt.
VI stage. The finish.
VII stage. Results.I stage. SDA (rules of the road).
a
tg 2 t + 1
e
1
v
tg t
well
cos t / sin t, t ≠ k, kZ.
d
sin2t + cos2t
and
1/ sin 2 t, t ≠ k, kZ.
yo
ctg t
To
1,t ≠ k / 2, kZ.
h
1+ctg2t
G
sin t /cos t, t ≠ /2 + k, kZ.
th
tg t∙ctg t
b
1/ cos 2 t, t ≠ /2 + k, kZ.
II stage. Inspection.
№
Expression
Answer options
A
V
WITH
1.
1 – cos 2 t
cos 2 t
-sin2t
sin 2 t
2.
sin 2 t - 1
cos 2 t
- cos 2 t
2 cos 2 t
3.
(cos t – 1)(1+ cos t)
-sin2t
(1+ cos t) 2
(cos t – 1) 2
III stage. Cross country racing.
IV stage. Sudden stop is an accident.
V stage. Halt.
2 "+" - score "4";
1 "+" - score "3".
The second - from the word "proud".
And you drive the third horses,
The fourth will be the bleating of a sheep.
My fifth syllable is the same as the first
The last letter in the alphabet is the sixth,
And if you guess right,
Then in mathematics you will receive a section like this.
(Trigonometry)VI stage. The finish.
VII stage. Results.